マッチ箱の脳(AI) -- パーセプトロン
はじめに
前回の「マッチ箱の脳(AI)」のネタで、今回は「パーセプトロン」を組んでみることにしました。
パーセプトロンとは
機械学習のアルゴリズムの1つで、ラベル付けされた多次元データを、ラベルごとに分類する境界を求めるアルゴリズムです。
以降は簡単のため、2次元データに対して2値のラベル(-1または+1)が付けられるケースに限定します。
例えば:
| label | x | y |
|---|---|---|
| +1 | -2 | 1 |
| +1 | -1 | 4 |
| +1 | 1 | 3 |
| +1 | 3 | 3 |
| -1 | -3 | -1 |
| -1 | 0 | -1 |
| -1 | 2 | 1 |
| -1 | 3 | 2 |
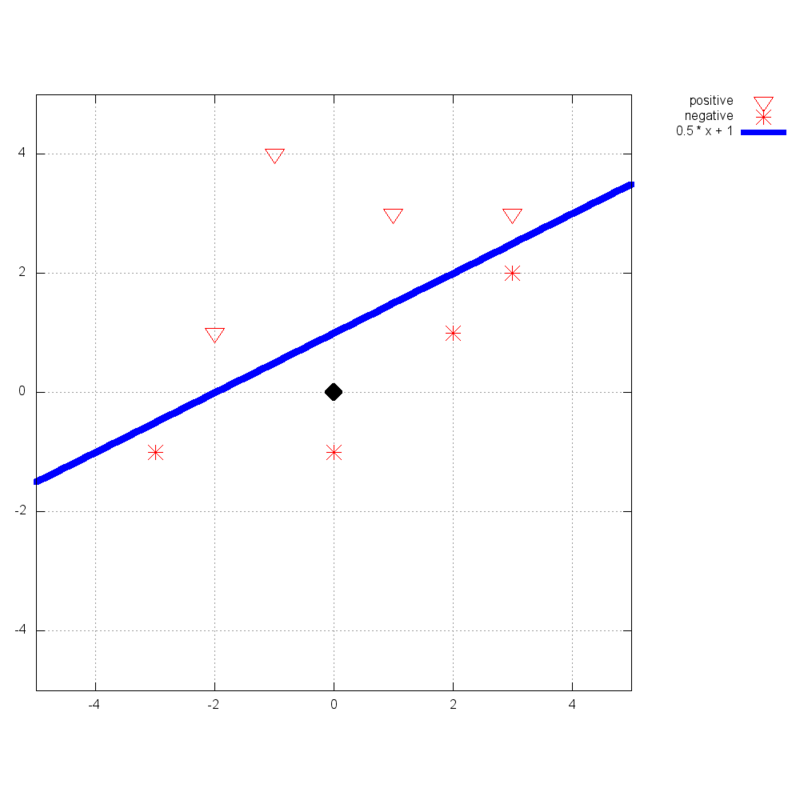
というデータに対しては、y = 0.5x + 1 が+1のデータと-1のデータを分類する境界となります。このような識別境界を求める手法の1つが、パーセプトロンです。
パーセプトロンのアルゴリズム
- \(ax + by + c = 0\) という直線を考える。\(a, b, c\)はランダムに初期化
- \(a, b, c\)が更新されなくなるまで、以下を行う:
- 各訓練データ\((x_i, y_i)\)について、
- \(k = ax_i + by_i + c \)を求める
- \(k\)が\(+\)だが訓練データのラベルが\(-\)である場合、\(a = a-x_i, b = b-y_i, c -= c-1\)と更新
- \(k\)が\(-\)だが訓練データのラベルが\(+\)である場合、\(a = a+x_i, b = b+y_i, c = c+1\)と更新
- 各訓練データ\((x_i, y_i)\)について、
上記が停止した時、\(ax + by + c = 0\)が識別境界となります。非常にシンプルです。なぜこの更新方法で良いのかについては、ちゃんとした理論があるようですが、正確に理解しているか怪しいので飛ばします- -;)
2次元データが「線形識別可能」、つまり直線により識別できるならば、上記のアルゴリズムは必ず停止し、答えが求まります。
例
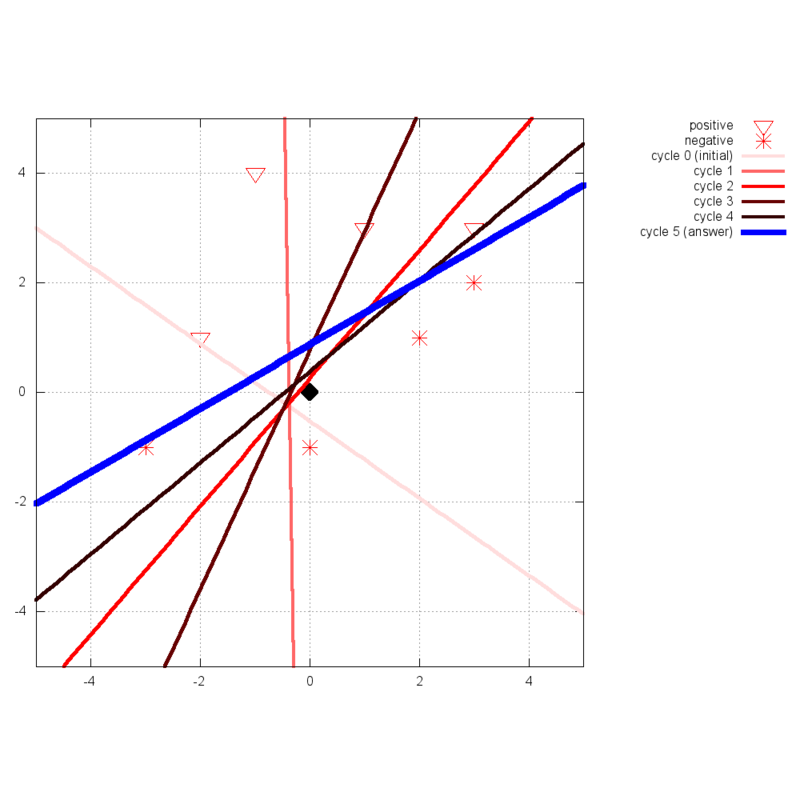
上述した例に対してパーセプトロンを適用した結果です。5回の更新で識別境界を求めることが出来ました。ちなみにその境界は、 y = 0.581*x + 0.878.最終的な解に至る過程(cycle 0 -- cycle 4)も記しています(色で区別してるだけなので見難いかも)
補足
サンプルのJavaScriptソースコード(Node.js). https://gist.github.com/danglingfarpointer/2fa56b9359ec2e260f6b